Margins, Kernels, and Control: Why I Still Love Support Vector Machines
If you’re just getting into machine learning, you’re probably hearing a lot about neural networks, random forests, or transformers. They’re powerful - no doubt.
But if you’re looking for a model that’s simple to understand, fast to train, and surprisingly powerful on real-world data, then you should absolutely know about Support Vector Machines (SVMs).
In fact, when I’m working with a small dataset or when I care more about getting the decision boundary right than squeezing out a few extra points of accuracy, I still reach for an SVM.
Here’s why.
💡 Why Start with SVMs?
SVMs are a great entry point to “serious” machine learning for a few reasons:
- 🧠 They’re intuitive: You’re literally just drawing a line (or a curve) that separates two groups - and trying to make that line as far away from both groups as possible.
- 🔍 They generalize well: The focus on maximizing margin helps prevent overfitting, especially when you don’t have much data.
- ⚙️ They give you control: You can tune just two parameters (
Candgamma) and get vastly different behaviors. - 🧪 They work well out-of-the-box: With the right kernel, they can handle very complex patterns with no need for feature engineering.
📏 What Does “Maximizing the Margin” Mean?
Let’s say you’re trying to separate apples from oranges on a 2D plot. You can draw a line between them - easy. But what if you draw the line just barely missing one of the oranges? That’s risky.
What SVMs do instead is try to draw the line that leaves the biggest possible “buffer zone” between the two classes. This “margin” means that small shifts in the data won’t immediately cause misclassification.
Think of it as giving your classifier some breathing room - a safety margin.
🔁 What If The Data Isn’t Linearly Separable?
Real-world data is rarely that clean.
That’s where the kernel trick comes in. Instead of working directly in the original space, SVMs map your data into a higher-dimensional space, where a linear separator does exist.
The best part? It does this without ever explicitly computing that high-dimensional transformation. That’s why it’s called a “trick.”
The most common kernel is the RBF (Radial Basis Function) kernel, which lets the model draw curved decision boundaries - perfect for real-world problems.
🔧 Controlling the SVM: Two Key Parameters
You don’t need to tune 50 hyperparameters. Just two:
1. C: Regularization Strength
This controls how much you want to avoid mistakes on the training set.
- Low
C: The model allows more mistakes to keep the boundary simple and smooth. - High
C: The model tries to classify every point correctly - even if that means drawing a complex boundary.
2. γ (Gamma): Kernel Influence
This controls how far each training point reaches in shaping the decision boundary.
- Low
γ: Each point has a wide influence - leading to smoother, broader boundaries. - High
γ: Each point has a tight influence - resulting in sharper curves and a higher chance of overfitting.
Together, C and γ shape the behavior of your SVM like two knobs on a sound mixer.
🖼️ Visualizing SVM in Action
To see how SVMs actually behave, I trained a model on the classic make_moons dataset - a 2D dataset that’s not linearly separable - and visualized how the decision boundary evolves as we tweak its two key hyperparameters.
Effect of C: Margin Tightening
First, I kept the kernel sensitivity (gamma) constant and animated how the margin and decision boundary change as C increases from 0.01 to 100.
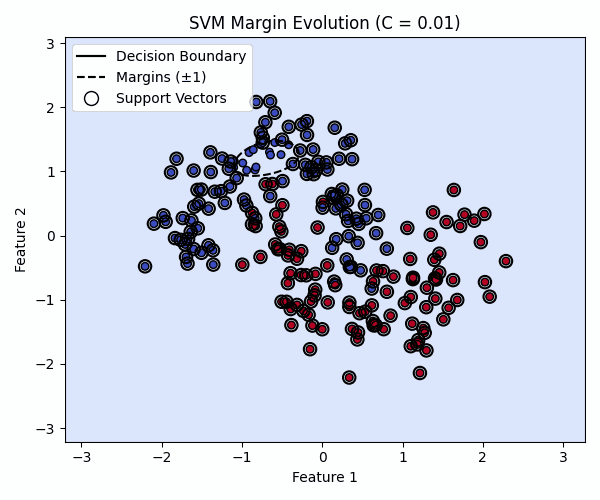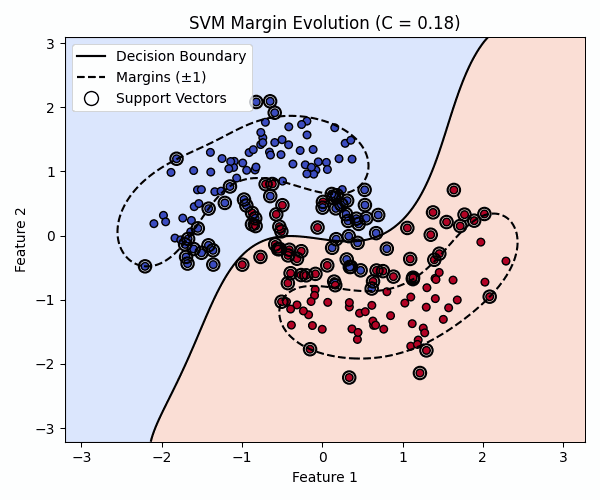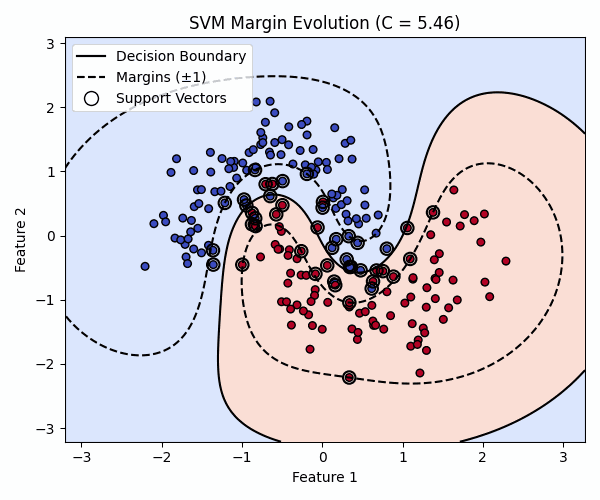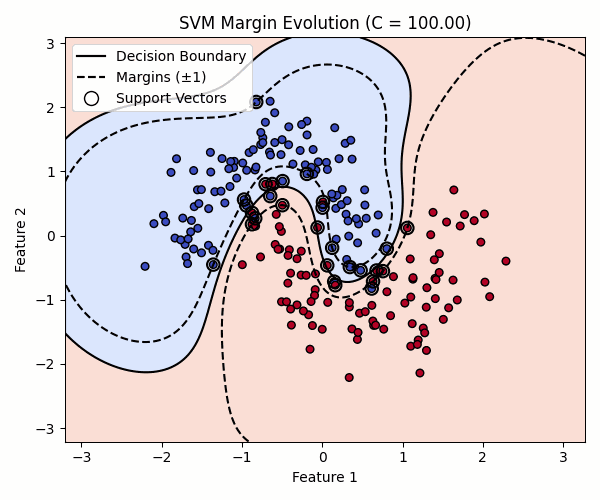
As C increases, the model becomes less tolerant of mistakes. The margin narrows, the boundary sharpens, and the number of support vectors often decreases as the model tries to fit the data more tightly.
Effect of γ: Kernel Flexibility
Next, I fixed C = 1.0 and varied gamma - which controls how much each training point influences the decision boundary.
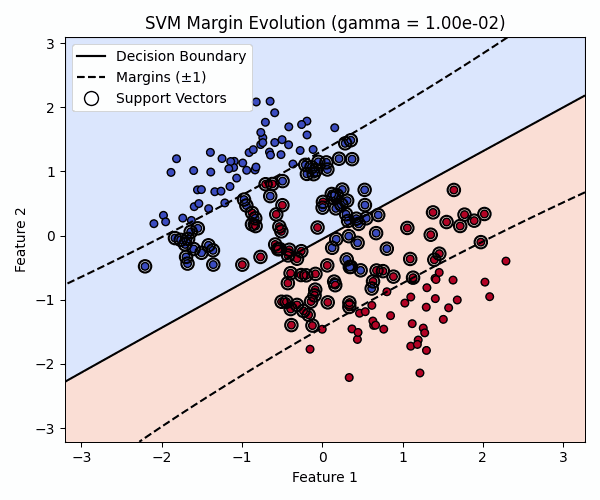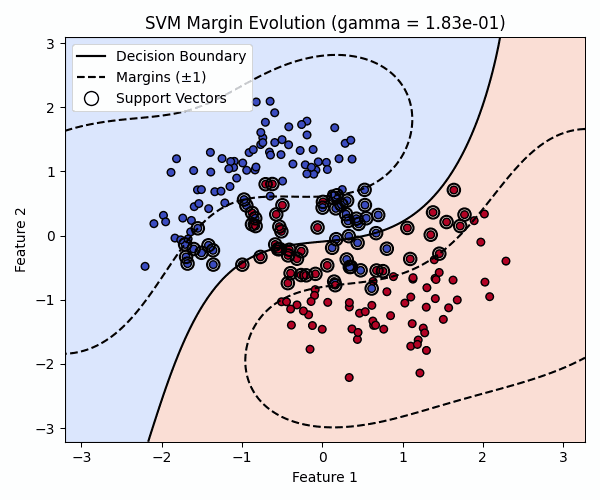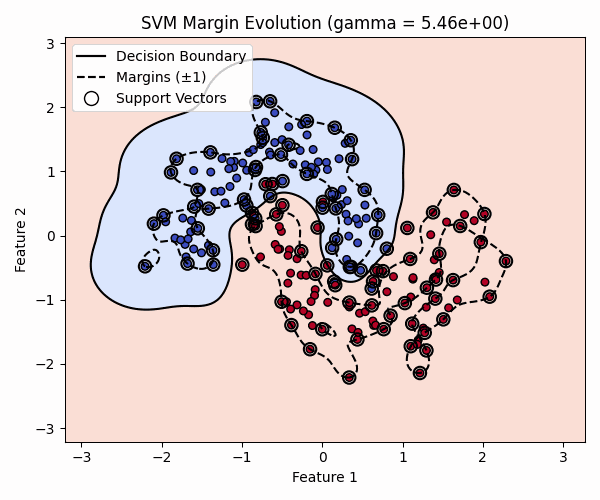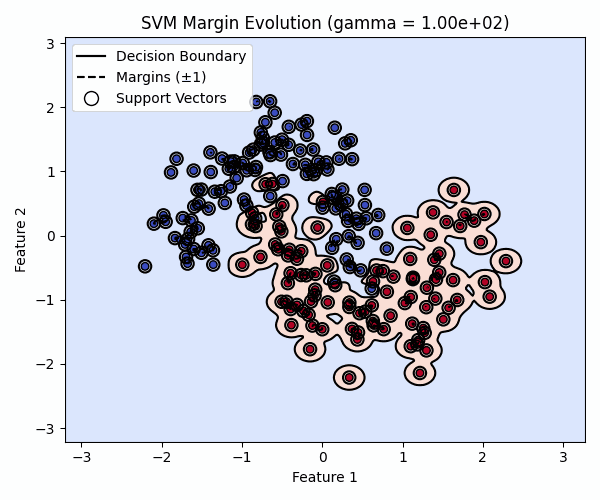
Lower γ values produce broad, smooth boundaries. Higher γ values lead to sharp, highly localized curves that can perfectly trace training data - but risk overfitting.
💻 Want to Try It Yourself?
Here’s the script I used to generate the visualization.
It uses:
scikit-learnfor the SVM and dataset generationmatplotlibfor plottingimageiofor generating the GIF
Feel free to change the dataset, try a different kernel, or animate gamma instead of C.
✅ When Should You Reach for an SVM?
SVMs are especially effective when:
- You have fewer samples but well-structured data
- You care about clear and stable decision boundaries
- You want a model that’s quick to train and easy to interpret
Even if you move on to deep learning later, understanding SVMs gives you a rock-solid foundation in decision theory, optimization, and kernel methods.
🚀 Final Thoughts
SVMs are like the hand tools of machine learning. Maybe not as flashy as a neural network, but elegant, precise, and always worth keeping in your kit.
They taught me how to think in terms of margins and generalization - and they still earn their keep in my projects.